Proyecto 1

1A. Reporte escrito: Experimentos y análisis

1. Introducción

En la era digital actual, el big data ha emergido como un recurso valioso para las organizaciones, permitiéndoles extraer, procesar y analizar datos significativos. El big data se caracteriza por sus cuatro V: volumen, velocidad, variedad y veracidad. El volumen se refiere a la gran cantidad de datos generados y almacenados; la velocidad, a la rapidez con la que se generan y procesan; la variedad, a los diferentes tipos de datos (estructurados y no estructurados); y la veracidad, a la calidad y precisión de dichos datos. La capacidad de manejar y analizar estos grandes volúmenes de información de manera eficiente es crucial para aprovechar al máximo el potencial del big data (Müller et al., 2016).

El análisis de big data permite a las organizaciones identificar patrones, predecir tendencias y optimizar procesos, lo que puede resultar en mejoras significativas en la eficiencia operativa y en la toma de decisiones estratégicas. Sin embargo, la manipulación de grandes volúmenes de datos presenta desafíos importantes en términos de infraestructura, almacenamiento, procesamiento y análisis. Los algoritmos eficientes son fundamentales para enfrentar estos desafíos y garantizar que los sistemas de big data funcionen de manera óptima (Manyika et al., 2011).

Este reporte se enfoca en comparar diferentes órdenes de crecimiento mediante simulaciones en un entorno de Jupyter. Se analizarán los siguientes casos: \(O(1)\) vs \(O(\log n)\), \(O(n)\) vs \(O(n \log n)\), \(O(n^2)\) vs \(O(n^3)\), \(O(a^n)\) vs \(O(n!)\) y \(O(n!)\) vs \(O(n^n)\). Para cada comparación, se seleccionarán rangos adecuados de \(n\) que permitan visualizar claramente las diferencias entre estos órdenes. Se generarán gráficas para cada caso y se discutirán las observaciones correspondientes. Además, se incluirá una tabla con tiempos de ejecución simulados para algoritmos ficticios asociados a los órdenes de crecimiento mencionados, utilizando distintos tamaños de entrada \(n\). Este análisis proporciona una visión clara de cómo los diferentes órdenes de crecimiento afectan el rendimiento y la eficiencia de los algoritmos.

2. Desarrollo

2.1 Bibliotecas utilizadas

import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt

2.2 Definición de funciones de crecimiento

def constant(n): return 1
def logarithmic(n): return np.log(n)
def linear(n): return n
def linear_logarithmic(n): return n * np.log(n)
def quadratic(n): return n**2
def cubic(n): return n**3
def exponential(n, a=2): return a**n
def factorial(n): return math.factorial(n)
def double_exponential(n): return n**n

2.3 Función de comparación de gráficos

def plot_comparison(funcs, labels, title, x_range):
    plt.figure(figsize=(7, 5))
    for func, label in zip(funcs, labels):
        plt.plot(x_range, [func(x) / 1e9 for x in x_range], label=label)
    plt.xlabel('n')
    plt.ylabel('Tiempo (s)')
    plt.title(title)
    plt.legend()
    plt.yscale('log')
    plt.xscale('log')
    plt.grid(True)
    plt.show()

2.4 Comparaciones entre órdenes de crecimiento

x_range_small = np.arange(1, 10)
x_range_medium = np.arange(1, 100)

# Comparación 1: O(1) vs O(log n)
plot_comparison([constant, logarithmic], ['O(1)', 'O(log n)'], 'Figura 1 - Comparación de O(1) con O(log n)', x_range_small)

# Comparación 2: O(n) vs O(n log n)
plot_comparison([linear, linear_logarithmic], ['O(n)', 'O(n log n)'], 'Figura 2 - Comparación de O(n) con O(n log n)', x_range_medium)

# Comparación 3: O(n^2) vs O(n^3)
plot_comparison([quadratic, cubic], ['O(n^2)', 'O(n^3)'], 'Figura 3 - Comparación de O(n^2) con O(n^3)', x_range_medium)

# Comparación 4: O(2^n) vs O(n!)
plot_comparison([lambda n: exponential(n, 2), factorial], ['O(2^n)', 'O(n!)'], 'Figura 4 - Comparación de O(2^n) con O(n!)', x_range_small)

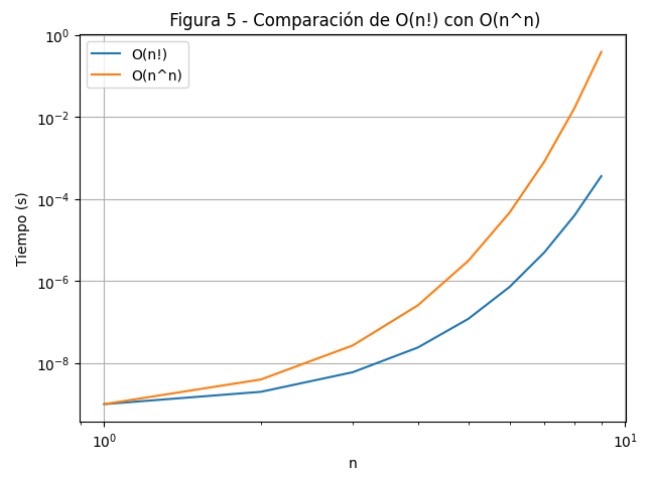
# Comparación 5: O(n!) vs O(n^n)
plot_comparison([factorial, double_exponential], ['O(n!)', 'O(n^n)'], 'Figura 5 - Comparación de O(n!) con O(n^n)', x_range_small)

2.5 Tabla de tiempos de ejecución simulados

Nota: Se creó una tabla con tiempos de ejecución simulados para algoritmos ficticios con los órdenes de crecimiento mencionados.

# Tamaños de entrada
n_values = [100, 1000, 10000, 100000]

# Funciones de costo
cost_functions = {
    'O(1)': constant,
    'O(log n)': logarithmic,
    'O(n)': linear,
    'O(n log n)': linear_logarithmic,
    'O(n^2)': quadratic,
    'O(n^3)': cubic,
    'O(2^n)': lambda n: exponential(n, 2),
    'O(n!)': factorial,
    'O(n^n)': double_exponential
}

# Elaboración de la tabla
results = []
for n in n_values:
    row = {'n': n}
    for label, func in cost_functions.items():
        try:
            row[label] = func(n) / 1e9  # Conversión a segundos
        except OverflowError:
            row[label] = 'Overflow'
    results.append(row)

import pandas as pd
df = pd.DataFrame(results)
df.set_index('n', inplace=True)
df

3. Análisis de Resultados

3.1 Interpretación de gráficos

3.1.1 Discusión de la Figura 1

El gráfico muestra que la función constante \(O(1)\) permanece constante independientemente del tamaño de la entrada, mientras que \(O(\log n)\) crece lentamente conforme \(n\) aumenta. Por lo tanto, un algoritmo con complejidad constante \(O(1)\) es más eficiente en términos de tiempo de ejecución en comparación con uno con complejidad logarítmica \(O(\log n)\).

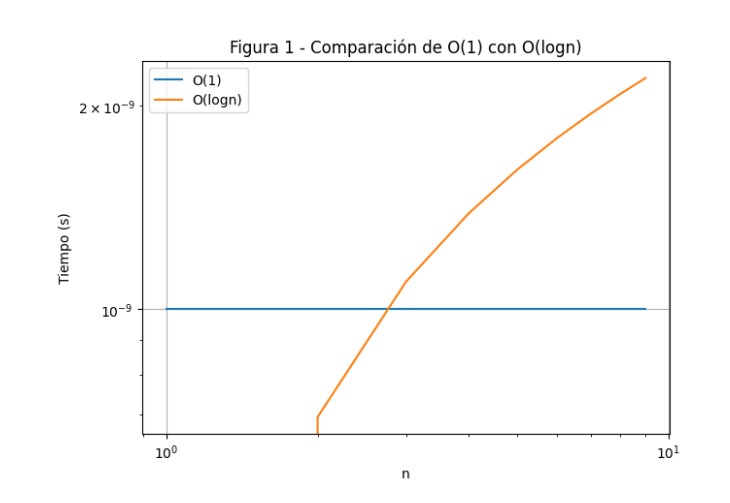
3.1.2 Discusión de la Figura 2

La función \(O(n)\) crece linealmente con el tamaño de entrada \(n\), mientras que la función \(O(n \log n)\) crece más rápido que \(O(n)\), pero sigue siendo práctica para valores moderados de \(n\). Por lo tanto, un algoritmo con complejidad lineal \(O(n)\) es más eficiente en términos de tiempo de ejecución en comparación con uno con complejidad lineal-logarítmica \(O(n \log n)\).

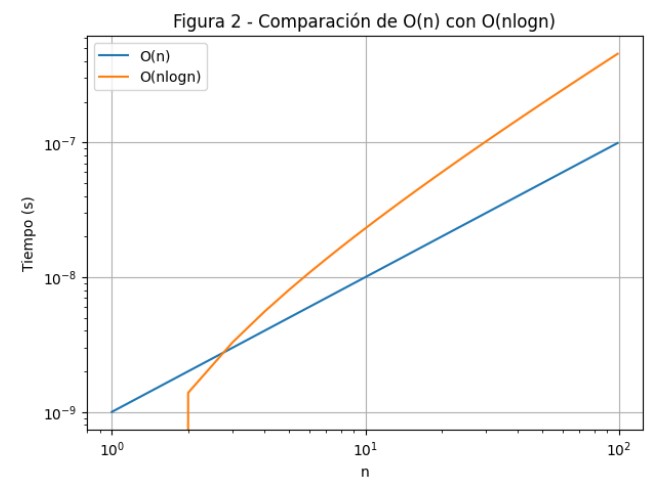
3.1.3 Discusión de la Figura 3

La función cuadrática \(O(n^2)\) crece más rápidamente que la lineal, pero la función cúbica \(O(n^3)\) lo hace aún con mayor rapidez. Por lo tanto, un algoritmo con complejidad cuadrática \(O(n^2)\) es más eficiente en términos de tiempo de ejecución en comparación con uno con complejidad cúbica \(O(n^3)\).

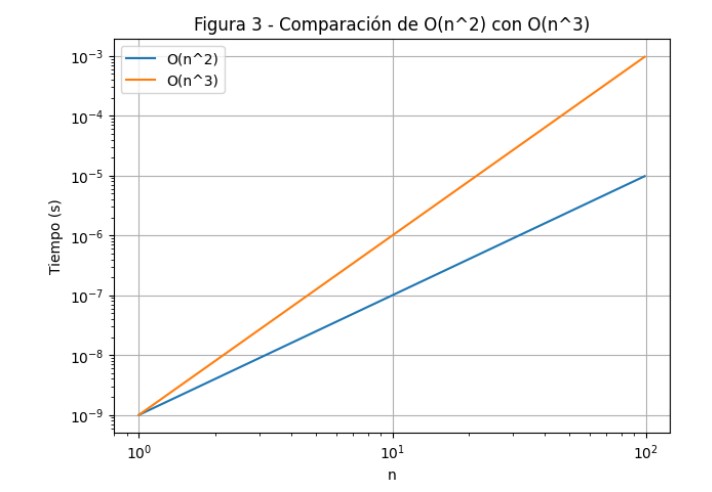
3.1.4 Discusión de la Figura 4

El gráfico muestra que la complejidad factorial \(O(n!)\) resulta en tiempos de ejecución mucho más altos que \(O(2^n)\) a medida que el tamaño de la entrada \(n\) aumenta. La complejidad factorial \(O(n!)\) crece considerablemente más rápido que la complejidad exponencial \(O(2^n)\), lo que hace que los algoritmos con esta complejidad sean prácticamente inutilizables para valores grandes de \(n\).

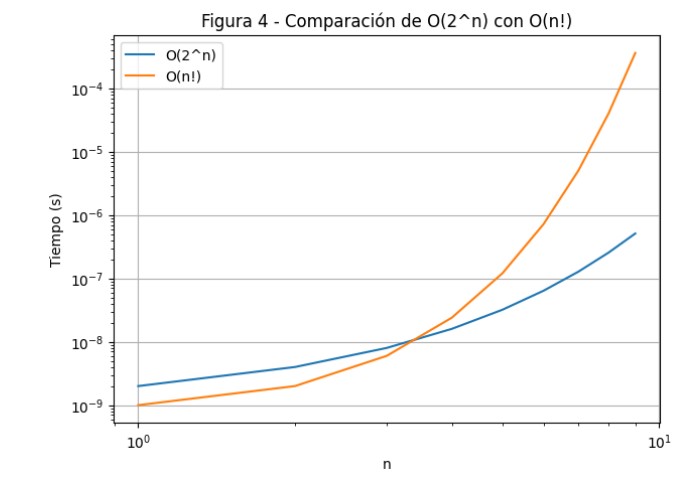
3.1.5 Discusión de la Figura 5

El gráfico muestra cómo la función factorial \(O(n!)\) crece muy rápidamente, pero la función doble exponencial \(O(n^n)\) crece aún más rápido a medida que aumenta el tamaño de la entrada \(n\). Por lo tanto, los algoritmos con complejidad factorial y doble exponencial son prácticamente inutilizables para valores grandes de \(n\).

3.2 Interpretación de la tabla

3.2.1 Tabla resumen de tiempos simulados

A continuación se presenta una tabla comparativa de los tiempos simulados para diferentes órdenes de crecimiento, utilizando distintos tamaños de entrada \(n\). Los resultados se expresan en segundos. En algunos casos, se muestra “Overflow” cuando el valor resultante excede los límites de representación.

Tabla 1. Tiempos simulados para diferentes órdenes de crecimiento de O(1), O(log n), O(n), O(n log n), O(n²)

n	O(1)	O(log n)	O(n)	O(n log n)	O(n²)
100	1.00e-09	4.61e-09	1.00e-07	4.61e-07	1.00e-05
1000	1.00e-09	6.91e-09	1.00e-06	6.91e-06	1.00e-03
10000	1.00e-09	9.21e-09	1.00e-05	9.21e-05	1.00e-01
100000	1.00e-09	1.15e-08	1.00e-04	1.15e-03	1.00e+01

Tabla 2. Tiempos simulados para diferentes órdenes de crecimiento de O(n³), O(2ⁿ)

n	O(n³)	O(2ⁿ)
100	1.00e-03	1.27e+21
1000	1.00e+00	Overflow
10000	1.00e+03	Overflow
100000	1.00e+06	Overflow

Tabla 3. Tiempos simulados para diferentes órdenes de crecimiento de O(n!), O(nⁿ)

n	O(n!)	O(nⁿ)
100	Overflow	Overflow
1000	Overflow	Overflow
10000	Overflow	Overflow
100000	Overflow	Overflow

Nota: Algunos valores como O(2ⁿ), O(n!) y O(nⁿ) para valores grandes de \(n\) generan cantidades inmanejables por el sistema, resultando en Overflow. Esto refleja la inviabilidad práctica de algoritmos con estas complejidades cuando se trabaja con grandes volúmenes de datos.

Como se muestra en la tabla, el tiempo de ejecución de O(1) no depende del tamaño de n. Este mantiene un mismo valor, lo que indica que su tiempo de ejecución es constante. Por otro lado, los valores de O(log n) aumentan lentamente a medida que n crece, lo cual es consistente con su comportamiento logarítmico. En el caso de O(n), los valores aumentan de forma lineal conforme n se incrementa. Los valores de O(n log n) aumentan más rápido que los de O(n), pero no tan aceleradamente como los de O(n²). Por su parte, O(n²) crece rápidamente a medida que n aumenta, y O(n³) lo hace de forma aún más acelerada, incluso con valores pequeños de entrada.

Durante la ejecución del código, algunos resultados aparecen como “Overflow”. Esto se debe a que las funciones O(2ⁿ), O(n!) y O(nⁿ) para valores grandes de n (como 10,000 o 100,000) generan números extremadamente grandes, lo que excede la capacidad de representación y manejo numérico en Python.

3.3 Implicaciones de costos de cómputo necesarios para manipular grandes volúmenes de información

La manipulación de grandes volúmenes de información presenta importantes desafíos debido a los costos de cómputo. Estos costos se relacionan con el gasto monetario, los recursos computacionales requeridos, el tiempo de procesamiento, el uso de memoria, el almacenamiento y el consumo energético. A continuación se presentan algunas de las implicaciones más relevantes:

• Infraestructura: Manipular grandes volúmenes de datos requiere una infraestructura robusta, que incluye servidores potentes, almacenamiento masivo y redes de alta velocidad. Esto representa costos elevados en hardware, mantenimiento y consumo energético (Armbrust et al., 2010).

• Energía: Los centros de datos que procesan grandes cantidades de información consumen enormes cantidades de energía, lo cual incrementa los costos operativos y contribuye al impacto ambiental debido a las emisiones de carbono (Baliga et al., 2011).

• Almacenamiento: El almacenamiento de grandes volúmenes de datos requiere soluciones escalables y eficientes. Este aspecto representa un costo considerable, ya que también debe garantizarse la recuperación oportuna de la información.

• Procesamiento: Procesar datos en tiempo real o en tiempo cercano al real implica el uso de algoritmos eficientes y de recursos de cómputo significativos. Estos costos pueden incrementarse especialmente al utilizar tecnologías como el aprendizaje automático y la inteligencia artificial (Wang et al., 2015).

En conjunto, la gestión de grandes volúmenes de información conlleva costos considerables en términos de infraestructura, energía, almacenamiento, procesamiento, seguridad y mantenimiento. Estos aspectos deben ser cuidadosamente planeados y gestionados para asegurar soluciones de big data eficientes y sostenibles.

4. Conclusiones

En las simulaciones realizadas se observó que los órdenes de crecimiento más bajos, como O(1), O(log n) y O(n), resultan altamente eficientes. Son ideales para tareas que demandan rendimiento óptimo y tiempos de respuesta reducidos.

Por otro lado, los órdenes de crecimiento O(n log n) y O(n²) demostraron ser prácticas y ampliamente aplicables, al ofrecer un buen equilibrio entre eficiencia y capacidad de procesamiento.

En contraste, las funciones con órdenes de crecimiento elevados como O(2ⁿ), O(n!) y O(nⁿ) resultaron ineficientes, generando tiempos de ejecución excesivos o incluso errores de memoria.

La tabla de tiempos de ejecución simulados confirma cómo el crecimiento del orden afecta directamente el rendimiento de los algoritmos. A mayor orden, mayor consumo de recursos y tiempo; a menor orden, mayor eficiencia en la ejecución.

5. Referencias

• Müller, V. C., Schal, J. M., Meyer-Lindenberg, A. (2016). Machine Learning for Brain Imaging. Cambridge University Press.
• Manyika, J., Chui, M., Brown, B., Bughin, J., Dobbs, R., Roxburgh, C., & Byers, A. H. (2011). Big data: The next frontier for innovation, competition, and productivity. McKinsey Global Institute. https://www.mckinsey.com/business-functions/mckinsey-analytics/our-insights/big-data-the-next-frontier-for-innovation
• Armbrust, M., Fox, A., Griffith, R., Joseph, A. D., Katz, R. H., Konwinski, A., et al. (2010). A View of Cloud Computing. Communications of the ACM, 53(4), 50–58. https://doi.org/10.1145/1721654.1721672
• Baliga, J., Ayre, R., Hinton, K., & Tucker, R. S. (2011). Energy-Efficient Telecommunications.
• Wang, L., Chen, Y., & Liu, Q. (2015). Big Data Processing: A Survey. Springer.

6. Cambios Realizados

6.1 Nota sobre correcciones realizadas

Los siguientes ajustes fueron aplicados al presente documento en atención a la retroalimentación recibida por parte del docente. Se atendieron los puntos señalados con el fin de mejorar la calidad formal y académica del reporte:

• Se uniformó el formato del documento, manteniendo una estructura clara y coherente entre secciones.
• Se corrigieron errores ortográficos y gramaticales, incluyendo el uso adecuado de comas y acentos.
• Las expresiones matemáticas fueron reescritas utilizando la notación correcta en formato de ecuación (LaTeX), como es el caso de \(O(1)\), \(O(\log n)\), \(O(n^2)\), entre otras.
• Se estandarizaron los encabezados de cada sección para facilitar la lectura y navegación del documento.

Estas modificaciones aseguran que el trabajo cumpla con los criterios de presentación solicitados y refleje un esfuerzo riguroso en la construcción y exposición del contenido.